技术文章 / Technical articles
如何校准接触角测量仪?接触角测量仪目前能够做到的精度是多少?
作为一种的理化分析仪器,正如粘度计、分析天平等仪器一样,接触角测量仪事实上也需要进行的调校或校准操作。通常建议接触角测量仪1年校准一次。
但是,接触角测量仪很长时间采用的校准工具是玻璃板。玻璃校准板与显微镜的分划板一样,采用刻蚀技术将标准角度的图片刻在玻璃板上,再通过测试标准角度值后,看接触角测量仪的精度。 通过如上的描述可以很容易看出,如上的操作事实上没有对接触角测量仪本身进行任何调校或校准,只是测试了一下标准图片,看一下角度值差多少。而这样的操作事实上只是看看接触角测量仪量角度这样的方法是否对。或精度能够达到多少?且不论这个精度到底是否对。
在上海梭 伦或美国科诺的相关文章中,我们已经对玻璃板进行测值精度判断的重在缺点进行过了描述,概括而言,主要是玻璃板是二维的体系,无法符合接触角测量的3维体系的测量,因而,也无法判断出来仪器的精度并进行仪器调校。
那么,接触角测量仪的校准需要调校的是什么?
通过接触角测量仪的原理,即接触角测量仪通常采用侧视条件下拍摄3D条件下的液滴的轮廓并采用相应的算法分析得到接触角值。根据光学成像原理,可以知道,3D条件下,镜头(相机)与被测物体(水滴)在成像视角、俯视与否情况、样品本身的上表面水平情况均会影响到终的角度值结果。因而,接触角测量仪的校准主要采用的工具是:
3D红宝石球校准工具。且同时要求红宝厂球的精度为微米级的。
而,接触角测量仪的校准包括:
1、通过校准样品台的水平,校准接触角测量仪;
2、通过校准镜头的水平,校准接触角测量仪;
因而,从硬件提供方面,接触角测量仪的校准需要包括:(1)3D红宝石工具;(2)样品台微米级调整水平;(3)镜头微米级水平调整。所以,如果不能够提供如上整套工具(缺一不可),则该接触角测量仪是无法进行校准的,也根本无法该接触角测量仪的测值精度的。
通常情况下,显微镜的放大率在接触角测量仪中通常的分辨率为4um左右,那么实现的精度通常能够的是0.01mm。而对于0.01mm的精度变化的图像,通常而言其接触角值精度为0.1度左右。如下表计算所示:
| 球直径 | 球半径 | 球高 | 半径-球高 | COSθ | θ弧度 | θ角度 |
| 5.05 | 2.525 | 4.025 | -1.49969 | -0.59394 | 2.206742 | 126.437 |
| 5.05 | 2.525 | 4.035 | -1.51 | -0.59802 | 2.211824 | 126.728 |
| 误差值 | 0.291 |
为此,对于接触角测量的精度的差别的一个为有效的方法为,通过测量微高度变化如0.01mm高度变化时,接触角的测试值的变化。这样的变化包括两个部分:
操作办法为接触角测试的图片中,球直径保持不变,此时,球冠的高度变化0.01mm,此时:
1、接触角测量仪所采用的算法能否判断出来图片中角度的变化值0.2-0.3度左右;(具体值根据计算所得略有变化)
2、接触角测量仪采用的算法对于两次不同高度的图片测试的值与理论值的偏差范围,也即接触角测量仪的精度本身。
如下显示的两张图片为小角度和大角度时两个不同的角度时的接触角测量仪捕捉的图片。
.png)
大小度,初始高度时的接触角测量仪测试图片
.png)
大角度时,高度变化0.05mm时接触角测量仪测试图片
.png)
小角度接触角值时,接触角测量仪测试初始高度时的图片
.png)
小角度接触角值时,接触角测量仪测试高度变化0.01mm时的图片
如上图片是通过上海梭伦技术的3D红宝石球校准工具实现的高精度高度变化以及采用上海梭伦接触角测量仪SL200KS测试所得。
通过采用圆拟合和阿莎算法,我们对如上图片进行了分析,具体结果如下所示:
| 球直径 | 球半径 | 球高 | 半径-球高 | COSθ | θ弧度 | θ角度 |
| 5.05 | 2.525 | 4.025 | -1.49969 | -0.59394 | 2.206742 | 126.437 |
| 5.05 | 2.525 | 4.035 | -1.51 | -0.59802 | 2.211824 | 126.728 |
| 误差值 | 0.291 |
| 球直径 | 球半径 | 球高 | 半径-球高 | COSθ | θ弧度 | θ角度 |
| 5.05 | 2.525 | 4.025 | -1.49969 | -0.59394 | 2.206742 | 126.437 |
| 5.05 | 2.525 | 4.035 | -1.51 | -0.59802 | 2.211824 | 126.728 |
| 误差值 | 0.291 |
通过如上数据可以明显看出
1、阿莎算法自动修正了重力影响,因而测试结果上显示为,测试结果值高于圆拟合所得的接触角测量值。
2、接触角测量值采用圆拟合时,可以做到的精度为0.147度左右。采用阿莎算法时,由于偏差值对比为圆拟合而非阿莎算法的增量值,因而,偏差低为0.192-0.525度左右。但从实际应用来讲,阿莎算法修正了重力影响,综合将表面张力与接触角进行分析,因而,实际中数据的科学意义更大。
3、阿莎算法与圆拟合均地分辨出了图像的区别,且方向。
如下提供了同样的图片采用国产的接触角测量仪分析软件所得的数据。
| 球直径 | 球半径 | 球高 | 半径-球高 | COSθ | θ弧度 | θ角度 |
| 5.05 | 2.525 | 4.025 | -1.49969 | -0.59394 | 2.206742 | 126.437 |
| 5.05 | 2.525 | 4.035 | -1.51 | -0.59802 | 2.211824 | 126.728 |
| 误差值 | 0.291 |
| 球直径 | 球半径 | 球高 | 半径-球高 | COSθ | θ弧度 | θ角度 |
| 5.05 | 2.525 | 4.025 | -1.49969 | -0.59394 | 2.206742 | 126.437 |
| 5.05 | 2.525 | 4.035 | -1.51 | -0.59802 | 2.211824 | 126.728 |
| 误差值 | 0.291 |
可以看出:
1、国产的接触角测量仪分析软件无法判断出高度增加后的角度变化或偏差值较高,特别是小角度时,增加高度,测值结果反而减少了。
因而,国产的接触角测量仪的软件的分析精度通常是略有扩大的情况。
2、国产的接触角测量仪软件Young-Laplace方程测值结果脱离实际值,如下提供两张分析结果图片,可以很明显看出分析结果没有重合度。
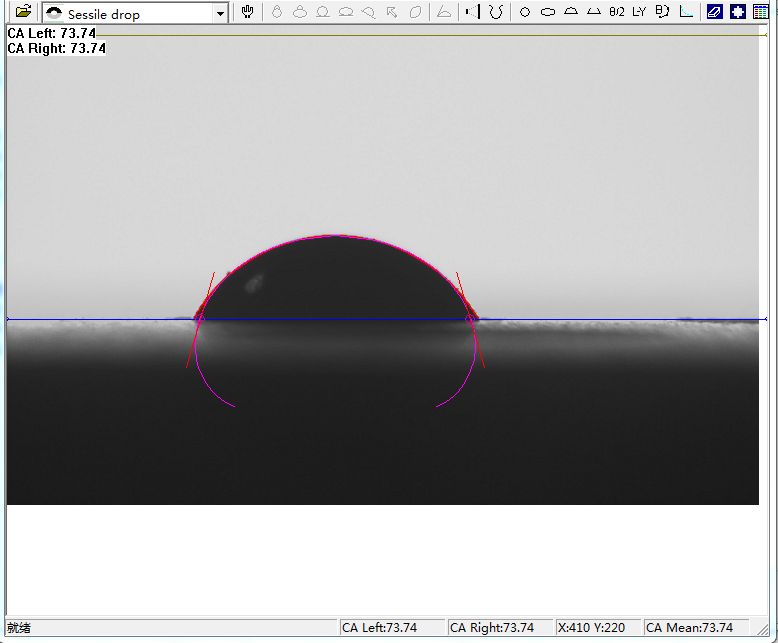
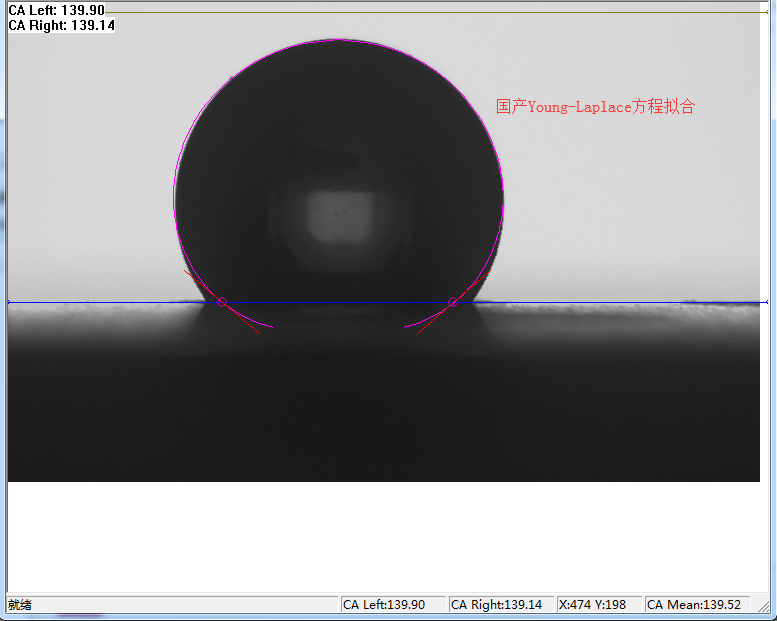
如下提供了国外的接触角测量仪分析软件的分析结果
| 球直径 | 球半径 | 球高 | 半径-球高 | COSθ | θ弧度 | θ角度 |
| 5.05 | 2.525 | 4.025 | -1.49969 | -0.59394 | 2.206742 | 126.437 |
| 5.05 | 2.525 | 4.035 | -1.51 | -0.59802 | 2.211824 | 126.728 |
| 误差值 | 0.291 |
| 球直径 | 球半径 | 球高 | 半径-球高 | COSθ | θ弧度 | θ角度 |
| 5.05 | 2.525 | 4.025 | -1.49969 | -0.59394 | 2.206742 | 126.437 |
| 5.05 | 2.525 | 4.035 | -1.51 | -0.59802 | 2.211824 | 126.728 |
| 误差值 | 0.291 |
通过结果可以看出:
1、在小角度时,Young-Laplace方程拟合算法成功率不高。如下所示:
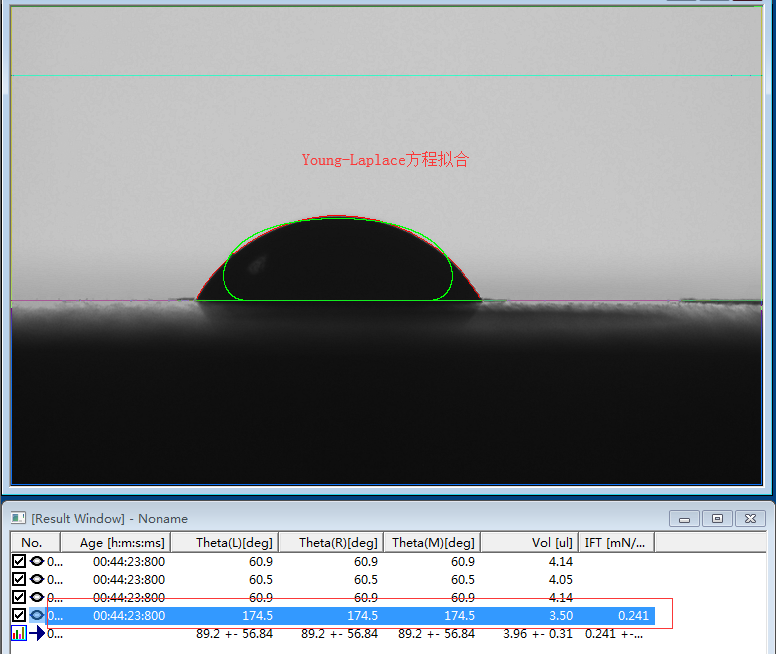
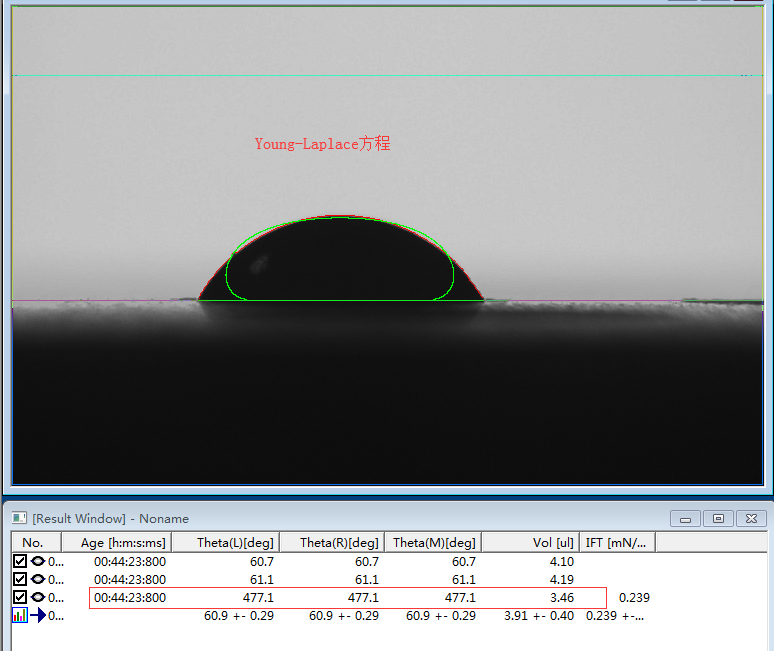
2、Young-Laplace方程拟合即使在真正的球的时候,或在轴对称时,事实上分析结果也不尽理想。在大度度时也无法分辨出角度的增量。
通过如上描述可以看出:
1、接触角测量仪的校准的前提是硬件;
2、接触角测量仪的精度以及分辨率的校准需要微米级精度的3D红宝 石球工具作出判断;
3、软件算法时,阿莎算法更具有科学性;
4、判断软件算法以及仪器精度的为科学的方法即可增加微米级变化量,看接触角测量仪的测值精度以及是否能够判断出来角度值的变化,以接触角测量值的变化方向与高度等实际几何值的变化量的方向是否一致。